Как рассчитать вероятность выигрыша в простых играх: полное руководство для начинающих
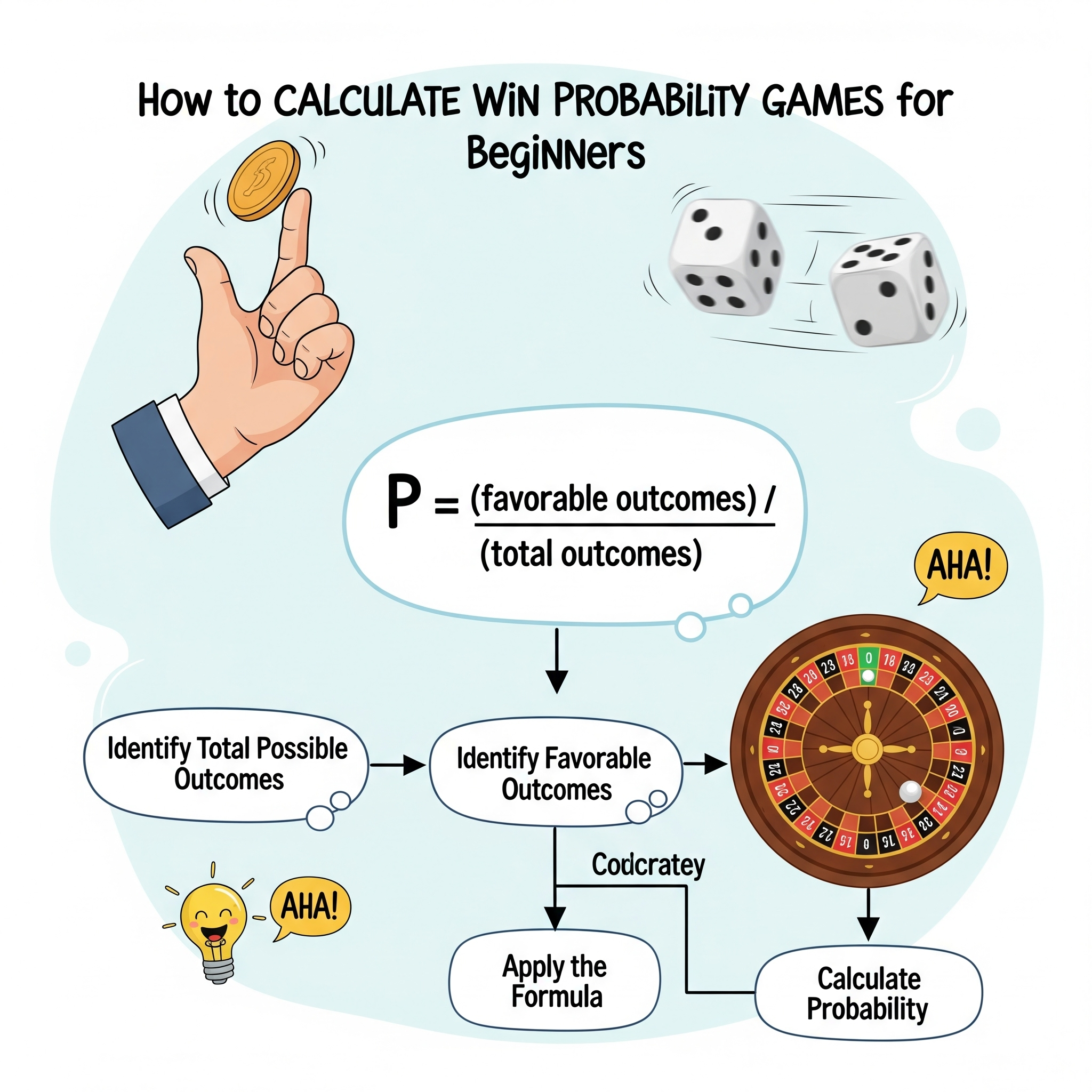
Понимание математики игр — ключ к осознанным решениям, будь то карточная игра с друзьями или анализ лотерейных билетов. Многие игроки в Казахстане полагаются на удачу, не зная, что за каждой игрой стоят точные математические закономерности. В этом материале разберём простые формулы расчёта вероятности выигрыша, рассмотрим конкретные примеры и научимся применять знания на практике.
Вероятность — это числовая мера возможности наступления события, выраженная от 0 (невозможно) до 1 (обязательно произойдёт). Умение рассчитывать шансы помогает принимать взвешенные решения и избегать необдуманных трат. Мы пройдём путь от основ теории до практических расчётов в популярных играх.

Основы теории вероятности в играх
Фундамент расчётов вероятности строится на понимании базовых принципов. Классическая формула выглядит просто: вероятность равна отношению количества благоприятных исходов к общему числу возможных исходов. Например, при подбрасывании монеты вероятность выпадения орла составляет 1/2 = 0,5 или 50%.
В игровом контексте благоприятные исходы — это варианты, при которых вы выигрываете. Общее количество исходов включает все возможные результаты игры. Важно учитывать, что события могут быть зависимыми или независимыми. При вытягивании карты из колоды без возврата вероятности последующих событий изменяются, а при бросании кубика каждый бросок независим от предыдущих.
Ключевые понятия для расчётов
- Элементарный исход — простейший результат эксперимента, который нельзя разложить на более простые
- Пространство элементарных исходов — множество всех возможных результатов
- Событие — подмножество пространства элементарных исходов
- Равновероятные исходы — исходы с одинаковой вероятностью наступления
- Несовместные события — события, которые не могут произойти одновременно
Понимание этих терминов критично для корректных расчётов. Многие ошибки в оценке вероятности возникают из-за неправильного определения пространства исходов или смешивания зависимых и независимых событий.
Практические формулы расчёта вероятности
Базовая формула классической вероятности: P(A) = m/n, где m — количество благоприятных исходов, n — общее количество равновероятных исходов. Эта формула работает для игр с чётко определёнными правилами и конечным числом исходов.
| Тип расчёта | Формула | Применение |
|---|---|---|
| Классическая вероятность | P = m/n | Кубики, карты, лотереи |
| Условная вероятность | P(A|B) = P(A∩B)/P(B) | Карты без возврата |
| Независимые события | P(A∩B) = P(A)×P(B) | Множественные броски |
| Противоположные события | P(не A) = 1 — P(A) | Вероятность проигрыша |
Формула для сложных событий
Когда игра включает несколько этапов или условий, используем правило произведения для независимых событий или правило сложения для несовместных событий. Правило сложения: P(A∪B) = P(A) + P(B) — P(A∩B). Для несовместных событий последний член равен нулю.
Комбинаторика помогает подсчитать количество исходов в сложных ситуациях. Основные формулы: размещения A(n,k) = n!/(n-k)!, сочетания C(n,k) = n!/(k!(n-k)!), перестановки P(n) = n!. Эти инструменты незаменимы при анализе карточных игр и лотерей.

Расчёт вероятности в конкретных играх
Рассмотрим популярные игры и их математический анализ. В игре в кости вероятность выпадения конкретного числа на одном кубике равна 1/6. Для двух кубиков ситуация сложнее: сумма 7 может получиться шестью способами из 36 возможных, значит P(сумма=7) = 6/36 = 1/6.
Карточные игры и их особенности
В стандартной колоде 52 карты. Вероятность вытянуть туза равна 4/52 = 1/13. Если первая карта — туз и мы её не возвращаем, то вероятность второго туза становится 3/51. Это классический пример зависимых событий, где исход первого розыгрыша влияет на вероятности последующих.
При игре в покер расчёты становятся сложнее. Вероятность получить пару в стартовой руке составляет примерно 5,9%. Для королевского флеша — около 0,000154%. Такие расчёты требуют глубокого знания комбинаторики и понимания структуры карточной колоды.
Лотереи и числовые игры
В простейшей лотерее типа «6 из 45» вероятность выигрыша джекпота равна 1/C(45,6) = 1/8145060 ≈ 0,000012%. Эта цифра наглядно показывает, почему лотереи — это скорее развлечение, чем способ заработка. Для лотерей с дополнительными числами расчёты усложняются пропорционально.
Важно помнить: математическое ожидание в большинстве азартных игр отрицательное. Это означает, что в долгосрочной перспективе игрок проигрывает больше, чем выигрывает.

Типичные ошибки при расчёте вероятности
Ошибка игрока — один из самых распространённых заблуждений. Многие верят, что после серии проигрышей вероятность выигрыша увеличивается. На самом деле каждое независимое событие имеет одинаковую вероятность независимо от предыдущих результатов. Монета не «помнит» предыдущие броски.
Неправильное понимание условной вероятности также приводит к ошибкам. Классический пример — задача Монти Холла, где интуитивное решение противоречит математически верному. После открытия пустой двери вероятность нахождения приза за оставшейся дверью становится 2/3, а не 1/2, как кажется на первый взгляд.
Проблемы с интерпретацией результатов
- Смешивание вероятности и математического ожидания
- Игнорирование размера выборки при анализе статистики
- Неучёт комиссий и скрытых расходов при расчёте реальной прибыли
- Применение формул для зависимых событий к независимым и наоборот
- Неправильное определение пространства элементарных исходов
Избежать этих ошибок поможет систематический подход: сначала определите тип события (зависимое/независимое), затем корректно посчитайте общее количество исходов, и только после этого применяйте соответствующую формулу.
Практические советы по применению знаний
Используйте расчёты вероятности как инструмент принятия решений, а не как гарантию результата. Даже при вероятности выигрыша 90% существует 10% шанс проигрыша. Планируйте бюджет исходя из возможных потерь, а не ожидаемых выигрышей.
Ведите статистику своих игр для проверки теоретических расчётов на практике. Отклонения от расчётной вероятности в короткой серии игр — это нормально, но в долгосрочной перспективе результаты должны приближаться к математическому ожиданию.
Инструменты для расчётов
Современные калькуляторы и приложения значительно упрощают сложные вычисления. Для базовых расчётов достаточно обычного калькулятора, но для анализа комбинаторных задач лучше использовать специализированное программное обеспечение или онлайн-калькуляторы вероятности.
Создайте собственную таблицу часто используемых вероятностей для быстрого доступа к информации. Включите вероятности для кубиков, карт, простых лотерей — это сэкономит время при принятии решений в реальных ситуациях.

Часто задаваемые вопросы
Влияет ли размер ставки на вероятность выигрыша?
Нет, вероятность выигрыша определяется правилами игры, а не размером ставки. Большая ставка увеличивает потенциальный выигрыш, но не меняет шансы на успех.
Можно ли увеличить вероятность выигрыша стратегией?
В играх, основанных исключительно на удаче (лотереи, рулетка), стратегия не влияет на вероятность. В играх со смешанными элементами удачи и навыка стратегия может повлиять на исход.
Как интерпретировать вероятность 1%?
Это означает, что из 100 одинаковых ситуаций событие произойдёт примерно в одном случае. Но это не гарантирует, что в конкретной серии из 100 попыток будет ровно одно благоприятное событие.
Почему математическое ожидание важнее вероятности выигрыша?
Математическое ожидание учитывает не только вероятность, но и размер выплат. Игра с высокой вероятностью выигрыша может быть невыгодной из-за маленьких призов относительно ставок.
Работают ли «системы» и «стратегии» в азартных играх?
В играх с фиксированной вероятностью (рулетка, лотерея) никакие системы не могут изменить математическое ожидание. Они могут влиять на распределение выигрышей и проигрышей во времени, но не на итоговый результат.
Понимание математики игр — это инструмент осознанного выбора, а не способ гарантированного обогащения. Используйте знания для контроля рисков и принятия взвешенных решений. Помните: в долгосрочной перспективе математика всегда берёт своё, поэтому относитесь к играм как к развлечению с заранее определённой стоимостью этого удовольствия.